There are several types of correlation coefficients from which to choose. The choice is based on the nature of the variables being correlated.

Point-Biserial Correlation 

When we have one variable that is measured on a continuous scale and one variable that is measured on a dichotomous scale, then the appropriate correlation technique is the Point-Biserial Correlation.  The calculation is straightforward with each of the categories in the dichotomous variable being given a value of either 0 or 1. The computational formula for the Point-Biserial Correlation Coefficient is:

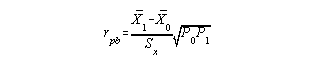
Phi

Once again the categories for each of the variables are given a value of either 0 or 1 and again the Pearson's Correlation is then applied to the data.  It should be noted that because the values 0 and 1 are arbitrary assigned to the categories the sign of the phi coefficient is of minimal use.   It only indicates which diagonal had the greater concentration of scores.  To estimate phi use the formula:
 

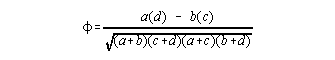
Phi coefficients in SPSS?

Since the phi coefficient is simply the special case of the Pearson Product Moment Correlation applied to two dichotomous variables, the coefficients produced by CORRELATIONS SPSS command are phi coefficients when two dichotomous variables are involved. 

Tetachoric Correlation

It is seldom used as it is a poor estimator of the population unless N is very large.

Spearman's Rho

In some cases we may ask subjects to rank items along two dimensions and we may wish to correlate these rankings.  Or it may be that the researcher decides to rank the data because of extreme data values.  To calculate a Spearman's rank order Correlation is quite simple in that once all data have been ranked,  then the Pearson Correlation formula is simply applied to the ranked data. Spearman's rho is a measure of the linear relationship between two variables.

Kendall's Tau Coefficient

Kendall based his statistic on the number of inversions in the rankings. Although there is evidence that Kendall's Tau holds up better than  Pearson's r to extreme nonnormality in the data, that seems to be true only at quite extreme levels. 

Kendall's Coefficient of Concordance (W)  Kendall's Coefficient of Concordance evaluates the relationship between a larger number of judges who rank the scores.